深度優先搜尋(DFS)是樹或圖的一種走訪方式,而我們也可以將他應用在「排列」上。
剪刀、石頭、布!-全部排列
現在有三個人:甲、乙、丙在猜拳,已知他們會出完全不同的拳,而你想知道依照甲、乙、丙的順序,他們出拳的排列有哪幾種的話,就可以用 DFS 來算喔!
蛤?用 DFS?這不是樹的走訪嗎?管他的,先上程式碼!
C++
string gesture[3] = {"剪刀", "石頭", "布"};
bool visited[3] = {false};
string arrangement[3];
void dfs(int layer){
if (layer == 3){
for (int i = 0; i < 3; i++){
cout << arrangement[i] << "\t";
}
cout << endl;
return;
}
for (int i = 0; i < 3; i++){
if (visited[i]){
continue;
}
visited[i] = true;
arrangement[layer] = gesture[i];
dfs(layer + 1);
visited[i] = false;
}
}Python
gesture = ['剪刀', '石頭', '布']
visited = [False] * 3
arrangement = [''] * 3
def dfs(layer):
if layer == 3:
print(*arrangement, sep='\t\t')
return
for i in range(3):
if visited[i]:
continue
visited[i] = True
arrangement[layer] = gesture[i]
dfs(layer + 1)
visited[i] = False輸出:
剪刀 石頭 布
剪刀 布 石頭
石頭 剪刀 布
石頭 布 剪刀
布 剪刀 石頭
布 石頭 剪刀解密時間!
到底為什麼我們可以用 DFS 來列出所有排列的可能呢?首先讓我們回想一下,我們平時在窮舉排列方法時會用的方法:先固定前面,再從最後面慢慢的替換。
比如說,求 1、2、3、4 的排列時,我們通常會先從 1234 出發,下一個變成 1243,再下一個則是 1324...以此類推,可以看到第一位數字都還沒被換掉,而第二位數字只換了一次,換最多次的是三、四位數字。
根據這樣的想法,我們可以發現 DFS 可以很容易的解決這個問題:將一位數字交由一層 DFS 來處理,而在每一層 DFS 中,我們要做以下這些事情:
- 檢查是不是最後一層,如果是的話,代表已經得到一組排列,應將結果輸出,並回到上一層
- 選定一個數字(代表欲排列物之編號),進行下一層的 DFS
讓我們看看 2. 這項敘述的詳細內容:首先是選一個數字,由於我們想讓每樣物品都輪過一次,所以我們使用 for 迴圈來依序取得編號。
接下來很重要的一點,因為有些東西我們可能已經排在前面了,所以我們要用一個陣列 visited[] 來儲存是否用過,如果已經用過,我們就要跳過這次迴圈,獲得下一個物品的編號。
若這項檢查通過的話,我們要進行以下動作:將這樣物品標示為已用過,再進行下一層的 DFS;而如果下一層的 DFS 已經結束並回到這層,記得要先將這層所使用的物品重設為沒有使用過,再進行下一個 for 迴圈或回到上一層 DFS。
說了這麼多,好像還是沒有好好的解釋為什麼 DFS 能夠勝任這樣的工作,這裡我就用一張圖來代表剛剛所做的全部事情吧,相信會突然變得很好懂。
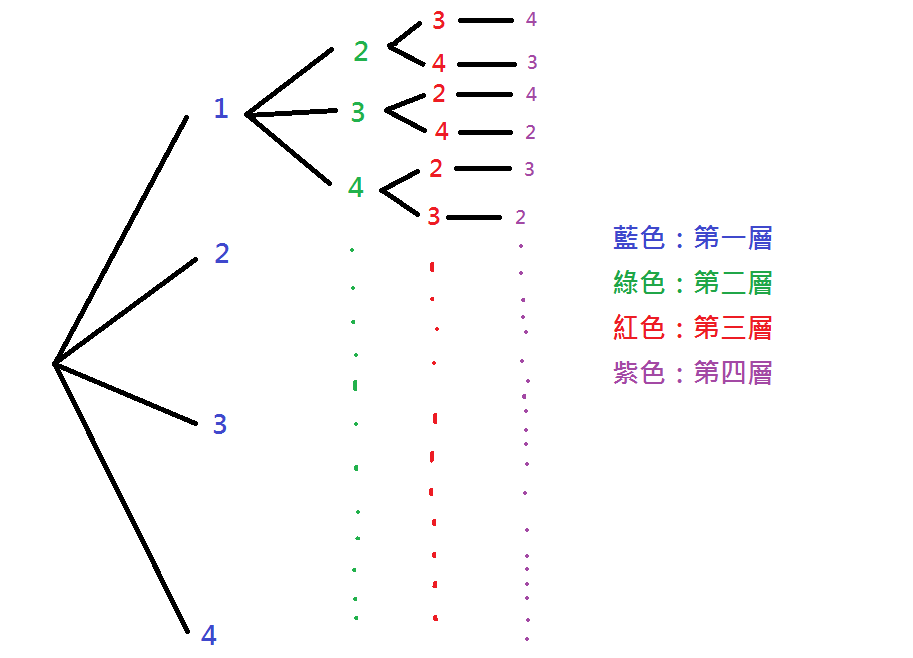
其實我們剛剛就是在對這個樹狀圖做 DFS,每次無路可走時,就代表找到了一種解法。應該滿好理解的吧?
那我們要進入下一個問題囉:要怎麼處理比較特別的排列?比如說物品不限使用次數的排列,或著有相同物的排列。
物品不限使用次數的排列,也就是上述的遊戲中,沒有限定三人一定要出不同的拳,想怎麼出就怎麼出。這種的比較簡單,也許你已經知道了,就是不要使用 visited[] 來記錄使用情況嘛!沒錯,所以我們只要把跟 visited[] 有關的部分全部砍掉就好了。
接下來的比較複雜(其實也還好):只能用特定數量來排列的有相同物之排列。
發放糖果-有相同物的排列
現在你手上有四顆糖果,分別是兩顆紅色且完全相同的、一顆藍色的,以及一顆黃色的,要分給甲、乙、丙、丁四人,會有哪些分法呢?
乍看之下好像有點複雜,因為要考慮那兩顆紅色的糖果,就算交換位置也還是一樣的分法,感覺好像要刪去一些分法,也很麻煩。這時可能會想說「畫個樹狀圖好了」,結果畫出來... 參差不齊的,根本很難對它做 DFS。
這時候,我們只要換一下想法就好,找出剛剛那個邏輯的不適合處加以替換。很顯然的,是我們用來記錄有沒有用過的 visited[] 陣列出了問題,因為對於紅色糖果來說,用掉一顆並不算真正的用完了,於是在這裡就會出現一些問題。那我們該怎麼處理呢?這裡就交給讀者們想囉。
誰是前三名?- n 物取 k 物的排列
最後我們來思考一下,n 物取 k 物的排列方法,也就是高中所學的 P 幾取幾。
班上有甲~戊五人是段考常勝軍,每次前三名一定是由他們其中三人組成的,能不能用 DFS 排出有幾種可能呢?當然是可以的,來想想看要怎麼處理吧。
首先是 visited[] 陣列,既然剛剛的案例似乎都是它出問題,這次也是嗎?不,這次不是它的問題,因為甲~戊這五人都是唯一的,所以並沒有違反當初我們使用 visited[] 的用意。
那麼應該也只剩下一個地方有疑點了:判斷是否為最後一層的地方。一直都沒思考這地方 if 判斷式裡的數字是怎麼來的,因為之前是有幾個要排就填多少,但這次我們只要取前三個,所以數字就填 3 吧。(沒錯,就是這樣)
先看程式碼應該比較好懂:
C++
bool visited[5] = {false};
int arrangement[3];
string people[5] = {"甲", "乙", "丙", "丁", "戊"};
void dfs(int layer){
if (layer == 3){
for (int j = 0; j < 3; j++){
cout << people[arrangement[j]] << " ";
} cout << endl;
return;
}
for (int i = 0; i < 5; i++){
if (visited[i]){
continue;
}
visited[i] = true;
arrangement[layer] = i;
dfs(layer + 1);
visited[i] = false;
}
}Python
visited = [False] * 5
arrangement = [''] * 3
people = ['甲', '乙', '丙', '丁', '戊']
def dfs(layer):
if layer == 3:
print(*arrangement, sep=' ')
return
for i in range(5):
if visited[i]:
continue
visited[i] = True
arrangement[layer] = people[i]
dfs(layer + 1)
visited[i] = False可以看到雖然有五個人在輪,但 if 判斷的地方只要跑 3 層 DFS 就會停止,這樣就可以達到我們只要取前三名的目的了。
動腦時間!
看了這麼多到底有沒有吸收到腦中呢?試著思考與回答這些問題吧:
下圖是最後這個程式執行結果的一部分,試問若把 if 判斷中的數字改為 2 的話,會不會造成輸出中有三組「甲 乙」、「甲 丙」...等情況,也就是只有下圖中的第三直行消失而已?為什麼會 / 不會?

- 你能簡單的歸納出 DFS 的步驟嗎?
能夠使用 DFS 列出 n 物取 k 物的組合種類嗎?如果可以,請實作看看;如果不行,試想想為什麼以及如何用別的方法解決。
試著找出排列與組合之間的關聯性。
- 有沒有不需要遞迴就能印出所有排列的方法呢?
後記:
終於打完這一篇了,看了看上次修改日期,嗯...原來是去年6月就應該要產出的啊,我又在耍廢了XD
至於後面的題目,算是一時興起的吧(欸),列出了我在寫這篇時突然想到的一些問題,可是我明明記得還有很多問題的啊,看來寫一寫就自動消失了呢,真不錯(是嗎
希望中間那個留給讀者思考不會被發現是我懶得打字。